BibTeX
@Article{Zhang2023,
author = {Zhang, Kaiyi and Zhou, Liang and Chen, Lu and He, Shitong and Weiskopf, Daniel and Wang, Yunhai},
journal = {Computational Visual Media},
title = {Angle-uniform parallel coordinates},
year = {2023},
issn = {2096-0662},
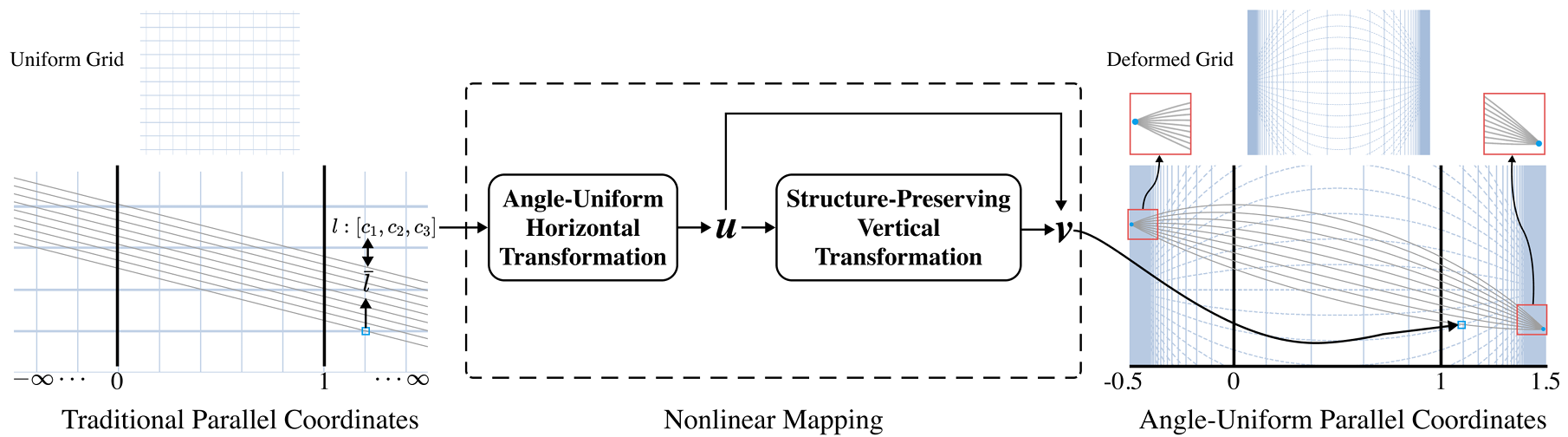
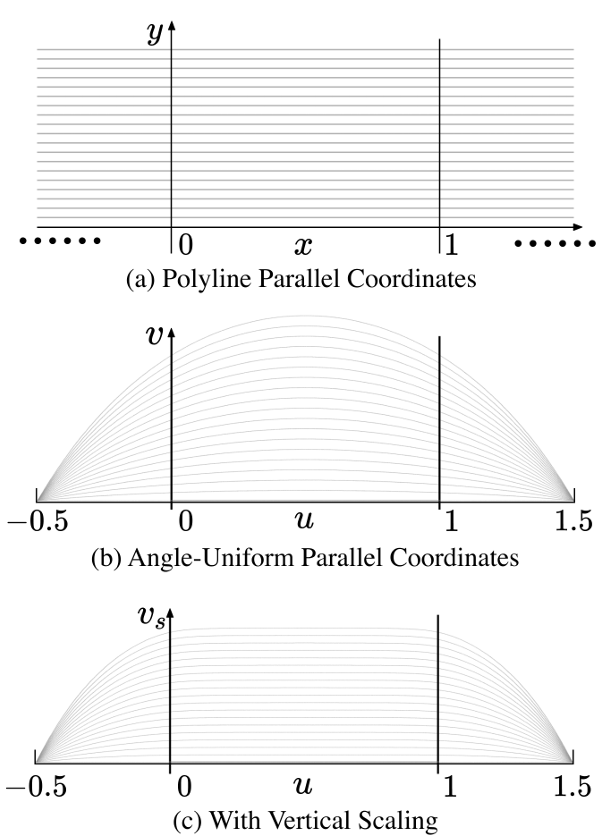
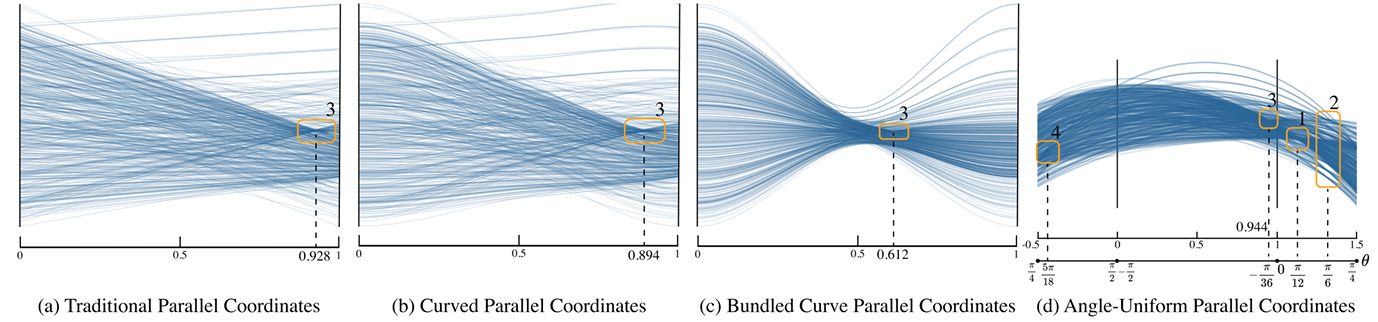
abstract = {We present angle-uniform parallel coordinates, a data-independent technique that deforms the image plane of parallel coordinates so that the angles of linear relationships between two variables are linearly mapped along the horizontal axis of the parallel coordinates plot. Despite being a common method for visualizing multidimensional data, parallel coordinates are ineffective for revealing positive correlations since the associated parallel coordinates points of such structures may be located at infinity in the image plane and the asymmetric encoding of negative and positive correlations may lead to unreliable estimations. To address this issue, we introduce a transformation that bounds all points horizontally using an angle-uniform mapping and shrinks them vertically in a structure-preserving fashion; polygonal lines become smooth curves and a symmetric representation of data correlations is achieved. We further propose a combined subsampling and density visualization approach to reduce visual clutter caused by overdrawing. Our method enables accurate visual pattern interpretation of data correlations, and its data-independent nature makes it applicable to all multidimensional datasets. The usefulness of our method is demonstrated using examples of synthetic and real-world datasets.},
doi = {10.1007/s41095-022-0291-7},
url = {https://doi.org/10.1007/s41095-022-0291-7},
}